Eigen & Matrix | Jinxi's Home

Notice that we will only consider real matrices in the following sections

Basic

Consider \(A \in M_n\), the basic definition of eigenvalues and eigenvector is \(Av = \lambda v\). The only constriant is that \(v\) must not be zero vector! And we construct the characteristic polynomial function:

\[\begin{aligned} \det( A-\lambda I) & =( -1)^{n}( \lambda _{1} -\lambda )^{n_{1}} \cdots ( \lambda _{r} -\lambda )^{n_{r}}\\ & =( -1)^{n}\left( \lambda ^{n} -tr( A) \lambda ^{n-1} +\cdots +( -1)^{n}\det( A)\right) \end{aligned}\]

notice that the characteristic polynomial function is a polynomial of order \(n\), we can conclude the following theorem:

\[\begin{equation} A\ \text{must have } n\text{ eigenvalues (they can be the same)} \end{equation}\] \[\begin{equation} \det(A) = \prod_i^{r} \lambda_i^{n_i} \end{equation}\] \[\begin{equation} tr(A) = \sum_i^{r} n_i\lambda_i \end{equation}\]

If \(A\) is diagonalizable, we have

\[\begin{equation} A = PDP^{-1} \end{equation}\]

where \(D\) is the diagonal matrix and \(P\) is an invertible matrix consists of corresponding eigenvectors. And if \(A\) is symmetric, we can find that \(P\) is orthogonal.

For matrix \(A, B \in M_n\), we say that \(A\) and \(B\) are similar if we can find an invertible matrix \(P\) such that \(P^{-1}AP = B\).

Take a look at References 1-4 for proof and extensions

A few facts to know

~~If the eigenvalues of a square matrix are all zeros, then the matrix is the zero matrix~~
Look at this one here: \(\begin{bmatrix} 0 & 1\\ 0 & 0 \end{bmatrix}\)
If a symmetric matrix has only zero eigenvalues, it is in fact a zero matrix.
Inverse dose not imply diagonalization, and vice versa.

Eigen & Transformations

One way of understanding matrices is to consider them as some kind of linear transformations, thus we need a set of basis to represent every transformation. And if we choose a distinct set of basis, the representation of the transformation would be distinct as well. As a result, the concept of similarity is introduced. The main idea is that if two matrices are similar, we can say that they are the same transformation in distinct representations with respect to corresponding distinct bases. A visual explanation in given below:

An explanation for similarity.

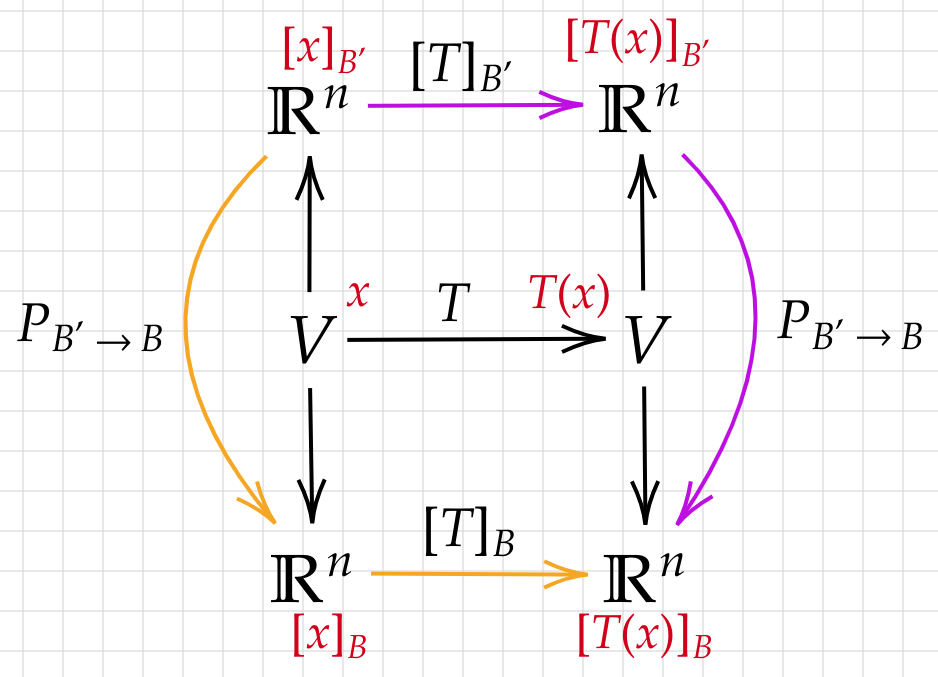
As a result, from my point of view, what eigen-decomposition is doing is to find a much simpler way to represent a kind of transformation in diagonal(scaling) form under a certain set of basis(the span of eigenvectors).

Eigenvalues and Rank

Given a matrix \(A \in \mathbb{R}^{n\times n}\), we have the following conclusions:

If zero is not an eigenvalue of \(A\), then \(A\) is in full rank.
\(\dim Eigenspace(\lambda=0, A) + rank(A) = n\) (see Reference 5).

For more, please take a look at Reference 6